
Plot of residuals from a linear model of 2005-6 approval of President Bush. Horizontal lines mark the limits of the 95% confidence interval for residuals.
A few weeks ago, I wrote several posts on outliers in survey research. The immediate cause was a 50% approval rating found by the Hotline poll in December. A few days later the ABC/Washington Post poll came in at 47%. However, other polls were generally around only 41-43% at that time. So I looked at how unusual each of these cases was here and here.
But what about low outliers? Democratic leaning analysts are quick to pounce on high outliers that make President Bush appear to be doing surprisingly well, and cry foul-- attributing the result as due to the partisan make up of the poll, its peculiar timing, or some other idiosyncratic cause for the unexpectedly good reading.
When an unexpected low reading comes in, these analysts are somewhat reluctant to question the validity of the new poll. Rather it is taken at face value to represent the actual low standing of the President.
And of course Republican analysts are exactly the same only reversed.
To some extent this represents pure partisan bias. But to some additional extent it represents the assumptions of the individual and his or her expectations-- usually shaped by their environment and the dominant expectations in that group.
Political scientists are no different. We all have our biases, except me of course-- I am purely objective in all things <;-). And we live in an overwhelmingly Democratic environment, as do most faculty. This is all the more reason why political scientists need to consciously consider how these biases of expectation can affect our analysis and the questions we raise. For example, I always code "vote" in a pro-Republican direction. Not because I necessarily root for Republicans, but because the expectation in political science is that variables are coded in a pro-Democratic direction. Perhaps that is because of alphabetical order. Or perhaps it reflects the dominant bias of the profession. By reversing the coding, I force myself to question every result simply because all the coefficients have the opposite sign of "normal" coding. This makes me stop and think, but doesn't change the quantitative implications of the analysis at all. Which is a long way of saying that when the new Pew Center for the People and the Press poll came out this week, I added it to my presidential approval data and ran the models as usual, the results of which appear here.
But as I looked at the data it was obvious that the Pew result was some kind of unusually low reading of President Bush's approval compared to most other polls. My model before the Pew poll arrived was that the President enjoyed (if that is the right word) a 43% approval rating. So a reading of 38% is 5% below what should be expected based on my model. When the Hotline arrived at 50%, that was some 8% above expectations at the time. The ABC/Washington Post poll that also seemed high was 4% above expectations. In both cases, they were unexpected enough to deserve some examination, or at least a blog post.
And so, if Pew is now 5% below the expected approval, it deserves to be looked at, and not simply passed over without comment.
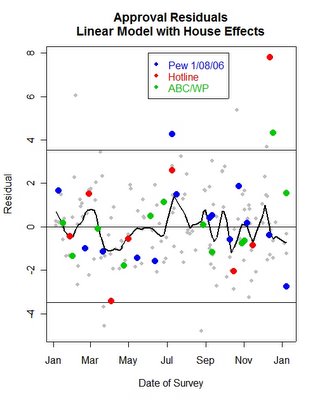
The graph above shows the residuals for all polls taken since January 1, 2005 using the linear model I have frequently employed in my analysis, most recently here. The results show that the new Pew poll is a little outside the 95% confidence interval. Over the course of the 175 polls taken prior to the Pew poll, 9 fell outside this interval. That is an empirical rate of .0514 compared to a theoretical rate of .0500. Not bad for social science. With the addition of the Pew poll, this proportion rises to .0568, still not bad agreement with statistical theory. This adds to my confidence that the model of approval is not systematically distorting results in some unexpected way. And it makes the Pew case look like a genuine outlier--- if not a huge one it is at least demonstrably unexpectedly low compared to what our model would predict.
Judged on exactly the same basis as the Hotline and ABC/WP polls, we should clearly discount the impact of the Pew poll in our analysis, at least to some extent.
It is striking that, just like Hotline and ABC/WP, the Pew polls are NOT generally outside the confidence interval for this model. Of 14 polls Pew has done in the last year, only this one falls outside the confidence interval. I wrote in the earlier posts that it is important to recognize outliers, but it is also important to distinguish between polls that are generally defective in some way, and polls that are perfectly well done according the the professional standards of polling, but which once in a while will produce an unexpected result. This is in fact guaranteed by statistical theory: the most perfectly designed and conducted poll imaginable will produce 1 outlier in 20 polls, on average. This is not to say we should ignore outliers-- quite the contrary. It is to say that we should look for, confirm and understand outliers and we should accept that these things happen (about 5% of the time.)
But there is one additional feature of the graph that pushed me to do another analysis. Only one Pew poll residual falls above the zero line in the residuals. This means that Pew polling, on average, registers somewhat lower approval of President Bush than does the "average" poll. This is not necessarily a point of concern. "House" effects are very common in polling. Different practices, different sampling, different interviewer training, different questionnairs and other things can create systematic and consistent tendencies for particular polls to average higher or lower approval ratings. For example, Gallup and ABC/WP produce results that are generally a little higher than the average result. The figure shows that Pew has the opposite house effect, one that is somewhat negative.
It is worth pausing to note that we can NEVER know which of these is truly correct and which is a house effect. Perhaps Gallup is biased (in the technical sense) upward in favor of the President. But it is just as reasonable that Gallup has it exactly right and other polls are generally biased (in the technical sense) downward. Unlike votes, we do not have a standard of truth to compare approval polls to.
I often take house effects into account when modelling presidential approval. I chose not to in the earlier Hotline and ABC/WP poll analyses because I wanted to include the house effects in the UNCERTAINTY about where approval really is, rather than statistically take it out. If we really don't know which house is right, then letting that variation add to our uncertainty about approval seemed (and seems) to me to be the right approach when assessing unexpectedly large or small outliers.
But there is some reason to wonder if the results here are simply because Pew has a house effect that is contributing to its interpretation here as an outlier. Likewise, perhaps I branded Hotline and ABC/WP polls as outliers in the earlier posts when their house effects could be confounding the case.
So I reestimate here a model that allows for house effects. The result of the estimation is that Pew has, over the past year, produced approval ratings that are expected to fall -3.70% below the readings of the ABC/WP poll, and -3.67% below the Hotline. Gallup, by comparison falls -.223% below ABC/WP and +3.48% above Pew. Again I stress that these are normal house effects and we should recognize this as a source of variation in our measurement of approval, but not use it to choose "good" and "bad" polls.
So what happens when we take house effects into account? The figure above presents the results. The new Pew poll is no longer an outlier, but has moved comfortably within the 95% confidence region. This is obviously sensible: if Pew has a house effect of -3.7%, and the new poll was -5% below the expected approval, then -5--3.7=-1.3% below the expectation based on the model. A residual of -1.3% is well within the range of random variation.
In contrast to Pew, the December Hotline and ABC/WP polls remain outliers even after house effects are taken into account. So whatever role house effects play, they don't account for those two polls.
But the Pew polls are now adjusted up to account for the house effect and produce a new outlier, this time one that is too high, compared to expectations at the time. That July poll was unusally high compared to other Pew polls, and the expectation at the time. When we account for the house effect, the high rating relative to other Pew polls becomes a high outlier compared to the model and all other polls.
So with or without the house effect adjustment, Pew has one outlier in 14 polls. Not quite 1/20 but for a small number of polls not a particularly surprising result. It just depends how you treat house effects for which poll is the outlier.
The evidence is clear that the current Pew poll is unexpectedly low compared to other polling that estimates about 43% approval. That seems in whole or in part due to the house effect of Pew polling. Still, I think we want to retain the uncertainty due to house effects in our models, rather than remove it via house effect estimates in this case. (Much of the time I DO think we should take out house effects, but that is a story for another day.) By that standard, the new Pew poll should be discounted somewhat, and we should continue to estimate an approval rate of about 43%.